微纳材料设计与制造研究中心

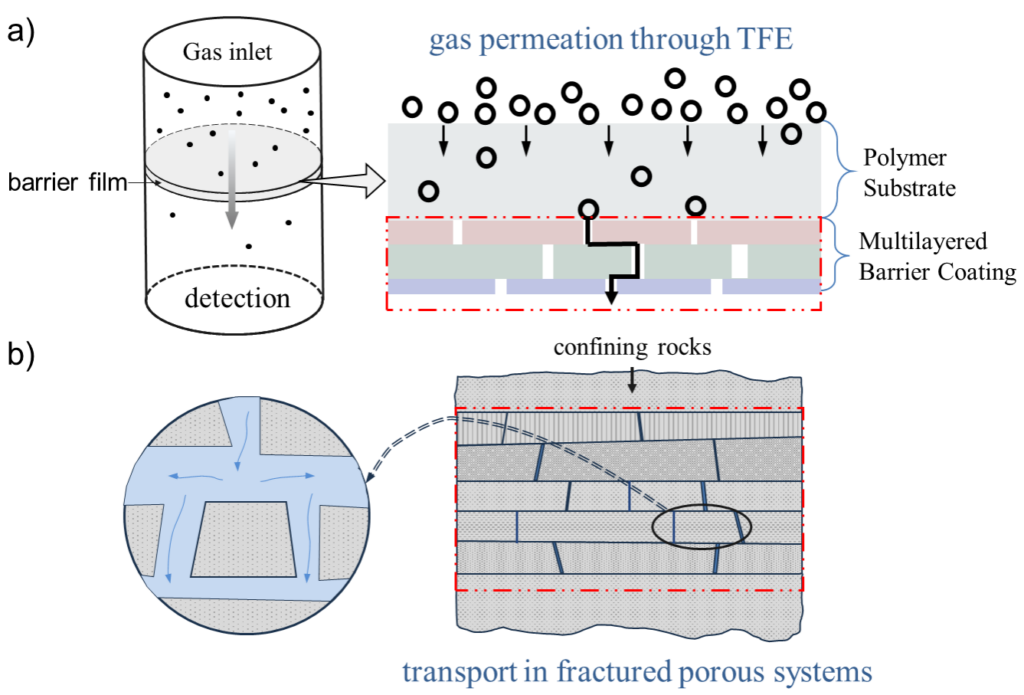
在柔性OLED等显示设备中，柔性阻隔膜具有屏蔽水汽的能力，是保护器件稳定运行的“隐形战士”。然而，当前对高阻隔膜性能的评估普遍周期长、成本高，如何快速准确地预测其稳态渗透速率，成为制约材料优化的核心瓶颈。为了提高评估效率、提取关键传质参数，亟需构建更精确的气体渗透描述模型。已有研究指出，阻隔膜中无机层存在的微观缺陷，会为气体分子提供“快速通道”（图1a），导致传输行为出现非经典动力学特征，进而削弱基于Fick定律的传统模型在拟合和预测方面的适用性。鉴于物质传输现象广泛存在于自然系统，研究团队将视野拓展至跨学科领域，向其它领域求取“真经”，发现分数阶扩散理论中的空间分数阶方程便能有效描述依赖介质内部快速扩散通道的传输行为。该方程已被Fomin等人成功用于描述地下水在多孔介质中的传输行为，并展现出优于Fick定律的建模效果^[1]。

图1 类比：（a）阻隔膜的无机叠层内由缺陷主导的物质输运；（b）地下水在多孔介质中的物质输运

受此启发，华中科技大学陈蓉教授的研究团队提出了一种基于空间分数阶扩散方程的高阻隔膜气体渗透模型。相关成果以“Defect-dominated gas permeation through high-barrier coatings modeled with fractional diffusion equations”为题发表在Industrial & Engineering Chemistry Research期刊上，硕士研究生田淞为第一作者，陈蓉教授、张晓东副教授为共同通讯作者。

团队首先针对最简单的叠层膜结构——单有机层+单无机层——探讨空间分数阶方程的适用性。采用并制备了PEN/AlO_x，并分别以H₂O和CO₂作为渗透气体在测试设备上获取相应的渗透测试曲线（图2a-b）。结果显示，随着数据量增加，拟合曲线逐渐逼近实验数据，且在同等数据条件下，引入分数阶机制的BSF模型拟合性能优于传统BF模型：在全数据拟合中（图2a-b）更精准，在预测方面（图2c-d）误差显著降低，尤其是在拟合数据有限的情境下更为突出。例如，仅用49.5%的H₂O非稳态数据进行拟合时，预测误差从约130%下降至约29%。

图2 BSF模型与BF模型在不同初始数据占比条件下对PEN/AlOx中H₂O和CO₂渗透过程的拟合效果（a-b）和稳态渗透率预测能力（c-d）对比分析。注：基于空间分数阶方程的模型记作bilayer-Fick-space-FDE (BSF)，基于Fick定律的模型记为bilayer-Fick (BF)

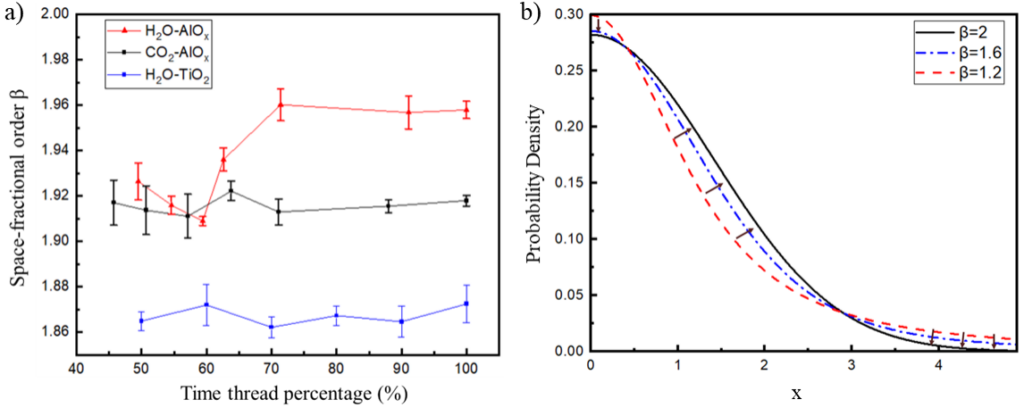
为了进一步理解模型中空间分数阶阶次β的物理意义，研究者分析了渗透过程中β值的变化趋势（图3a），观察到H₂O与CO₂在渗透过程中存在明显差异：在渗透的前期至中期阶段（约60%）之前，两者的β值均约为1.92，随后开始出现分化：CO₂维持稳定，而H₂O的β值则明显上升，增幅约为2%。结合AlO_x的化学性质，推测研究推测，该变化可能源于H₂O对AlO_x的腐蚀，即H₂O逐步破坏无机层结构，从而影响粒子扩散行为。这一推论也与Nehm^[2] 和Lee^[3] 等人对AlO_x结构变化的观察相吻合。根据分数阶扩散方程的相关理论，空间分数阶阶次β（0 < β ≤ 2）控制扩散过程中不同跳跃距离的概率密度曲线（图3b）。当β上升时，长距离跳跃与短距离跳跃的概率差异减小，密度分布曲线变得更加平缓。根据以上分析，猜测H₂O与AlO_x的化学反应使膜内缺陷的空间或尺寸分布更趋均匀，影响了粒子扩散的行为，体现在了β值的变化中。为进一步验证该猜测，研究者将无机层AlO_x替换为更耐水腐蚀的TiO₂，获取并分析H₂O渗透PEN/TiO₂的测试数据。经对比发现，对应曲线H₂O-TiO₂并没有呈现出上述变化趋势（图3a），一定程度验证了以上假设。这种β与扩散介质的结构非均匀性之间的关系，也曾在水文学系统的研究中被发现^[4]。这也提示我们，β可能成为判断膜结构变化的新“探针”，尽管它们之间的具体对应关系仍有待对微观缺陷结构进行大量细致的表征与分析。

图3 a）渗透过程中不同阶段空间分数阶阶次的变化：渗透气体种类与阻隔涂层材料的影响；b）跳跃距离的概率密度曲线随β的变化趋势：当β接近2时，极大或极小跳跃距离的概率降低，大量粒子跳跃距离的差异化减弱。注：β=2时，空间分数阶扩散方程退化到Fick定律

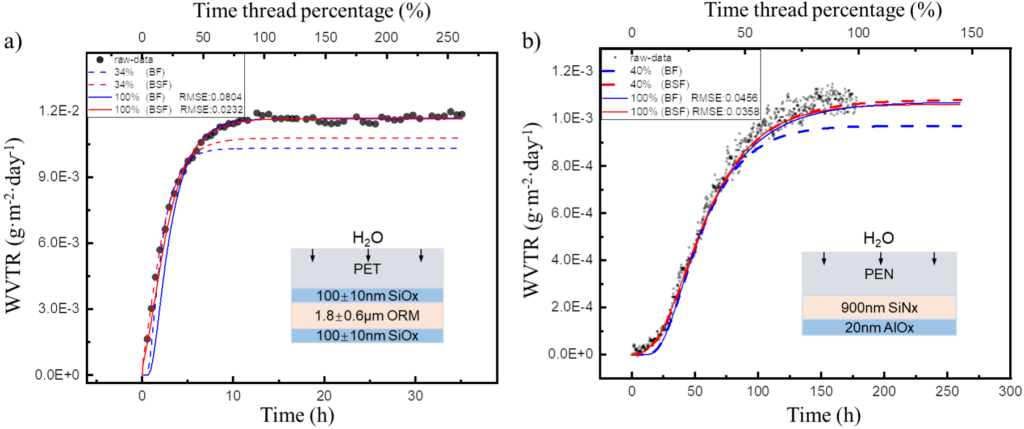
考虑到实际柔性OLED封装中多采用多层结构以延长水氧渗透路径、形成更复杂的扩散通道，研究团队进一步将BSF模型拓展应用至两种典型的多层阻隔膜系统，对其水汽透过率（WVTR）实验数据进行拟合与预测验证（图4）。结果显示，BSF模型在整体拟合精度和初期渗透阶段的表现均优于BF模型，能更准确反映优先通道引起的快速传输行为。在预测性能方面，BSF模型分别基于34.6%、40%的数据实现了6.08%、1.89%的低误差预测，均优于BF模型对应的10%、10.4%的偏差，进一步验证了其在复杂结构下的适用性与准确性。

图4 H₂O在不同多层结构阻隔膜中的渗透过程：a）覆盖在PET基底上的SiO_x/ORM/SiO_x三层结构，其中ORM指的是ORMOCER^®，一种有机-无机杂化高分子材料；b）覆盖在PEN基底上的AlO_x/SiN_x双层结构。

综上所述，空间分数阶扩散方程在表征缺陷主导型气体渗透过程中相较于Fick定律展现出显著优势。基于该方程构建的BSF渗透模型不仅有效提升拟合精度和预测能力，还适用于多种阻隔系统（如PEN/AlO_x、PEN/TiO₂及多层结构的复合阻隔膜）。更重要的是，模型中的阶次β为缺陷分布的定量刻画提供了新的思路。该工作为快速、精准评估高阻隔膜的WVTR提供了新工具，也为探究缺陷主导渗透机制提供了理论支撑与研究新思路。

[1] Fomin S A, Chugunov V A, Hashida T. Non-Fickian mass transport in fractured porous media [J]. Advances in Water Resources, 2011, 34(2): 205-14.

[2] Nehm F, Klumbies H, Richter C, Singh A, Schroeder U, Mikolajick T, et al. Breakdown and Protection of ALD Moisture Barrier Thin Films [J]. ACS Applied Materials & Interfaces, 2015, 7(40): 22121-7.

[3] Lee S, Jeon Y, Oh S J, Lee S-W, Choi K C, Kim T-S, et al. Study of mechanical degradation of freestanding ALD Al₂O₃ by a hygrothermal environment and a facile protective method for environmentally stable Al₂O₃: toward highly reliable wearable OLEDs [J]. Materials horizons, 2023, 10(10): 4488-500.

[4] Zhang Y, Benson D A, Reeves D M. Time and space nonlocalities underlying fractional-derivative models: Distinction and literature review of field applications [J]. Advances in Water Resources, 2009, 32(4): 561-81.